
The two variables would be outside temperature and ice. As my small tool of visualisation I used Power BI. Marine biologists warn that the growing number of powerboats registered in Florida threatens the existence of manatees. Example 1 This is a scatter plot showing the amount of sleep needed per day by age. Assess Have the students plot a number of points and look for a relationship. Here are the scatter plots I showed in class on Monday (the graphs were also posted and discussed on this USA Today blog). These two scatter plots show the average income for adults based on the number of years of education. In the real world, many things are related to each other. Once you've narrowed down which method you'll use, use your datasets to calculate their correlation. A common way of displaying bivariate data when both variables are quantitative is using a scatter plot. Now let's be sure Orion's pants don't fall down. More advertising costs lead to more sales. Examples 1 to 3 of Real-Life Correlations. The mean value in this situation lies at the left side of the peak value. As an example of what happens when you omit some data, be that because you purposefully want to create a misleading data visualization or you simply want to make your work easier, take a look at the scatter plot below. Visual Inspection mistakes and Illumination levels. Open the worksheet and click the Add-ons menu button. What is Considered to Be a “Strong” Correlation?Ĭorrelation vs.Practice looking for relationships with the students. What is Considered to Be a “Weak” Correlation? number of movies watched, it may look like this:
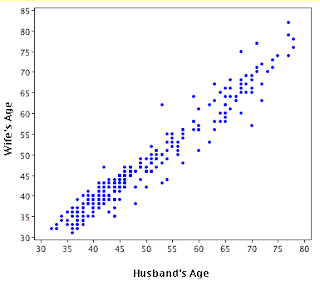
If we created a scatterplot of shoe size vs. In other words, knowing the shoe size of an individual doesn’t give us an idea of how many movies they watch per year. The shoe size of individuals and the number of movies they watch per year has a correlation of zero. IQ level, it may look something like this: If we created a scatterplot of daily coffee consumption vs. In other words, knowing how much coffee an individual drinks doesn’t give us an idea of what their IQ level might be. The amount of coffee that individuals consume and their IQ level has a correlation of zero. ice cream sales, it may look something like this:Įxample 1: Coffee Consumption vs. If we created a scatterplot of temperature vs. In other words, when it’s hotter outside the total ice cream sales of companies tends to be higher since more people buy ice cream when it’s hot out. The correlation between the temperature and total ice cream sales is positive. weight, it may look something like this:Įxample 2: Temperature vs. If we created a scatterplot of height vs. In other words, individuals who are taller also tend to weigh more. The correlation between the height of an individual and their weight tends to be positive. exam scores, it may look something like this:
#Scatter plot examples real life tv#
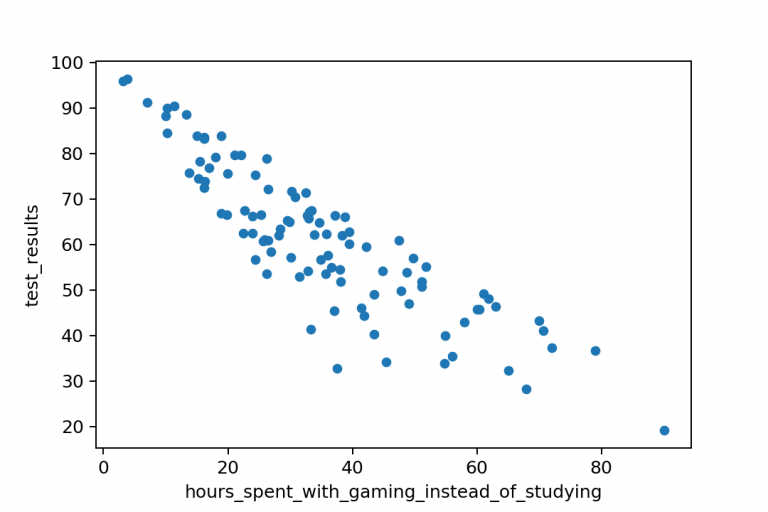
If we created a scatterplot of time spent watching TV vs. As time spent watching TV increases, exam scores decrease. In other words, the variable time spent watching TV and the variable exam score have a negative correlation. The more time a student spends watching TV, the lower their exam scores tend to be. body fat, it may look something like this:Įxample 2: Time Spent Watching TV vs. If we created a scatterplot of time spent running vs. As time spent running increases, body fat decreases. In other words, the variable running time and the variable body fat have a negative correlation.

The more time an individual spends running, the lower their body fat tends to be. Negative Correlation ExamplesĮxample 1: Time Spent Running vs. The following examples illustrate real-life scenarios of negative, positive, and no correlation between variables. 1 indicates a perfectly positive linear correlation between two variables.0 indicates no linear correlation between two variables.-1 indicates a perfectly negative linear correlation between two variables.The value for a correlation coefficient is always between -1 and 1 where: In statistics, correlation is a measure of the linear relationship between two variables.


 0 kommentar(er)
0 kommentar(er)
